待续
(原创,转发须注明原处)
算法是个很奇妙的东西,不管在招聘的笔试还是面试中,也不管你是学的什么语言或者什么方向的编程,出题者或面试官总会问问,尤其是关于排序算法的问题,对滴,在这次秋招中,我就被面试官问了无数次(有点夸张)。下面,我就好好总结总结下,我相信,以后绝对有人用得上的,方便点。。。
一、关于排序的概念
对的,就是概念,要学好一个东西,必须要先搞清概念,别一上来就看题敲代码,这是初学者浮躁的表现(我当初就是这样的),总想急于求成,想快点做点东西,当时确实学到了不少零碎的知识,但随着内容的深入与扩充,发现自己学的东西变得多而杂了,于是,又花更多的时间去理清知识体系。所以,我劝大家应该有个好的起点,从开始就弄清自己到底要学啥,学了些啥,有个清晰的知识体系会有助于我更好的深入。废话就不多说了。。。
-
- 内排序与外排序:简单地说就是,如果被排序的文件或数据适合放在内存中,则该排序就是内排序;而从磁盘或磁盘上进行排序的方法,则称为外排序。二者主要的区别:内排序可以很容易地访问任意元素,而外排序则必须顺序访问元素(至少大数据块是这样的)。
- 稳定排序与不稳定排序:稳定排序就是就是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同;不稳定排序则就相反了。(注:选择排序、快速排序、希尔排序、堆排序不是稳定的排序算法,而冒泡排序、插入排序、归并排序和基数排序是稳定的排序算法)
- 时间复杂度与空间复杂度:(这2个概念就不讲了,我就列出部分排序算法的时间复杂度和空间复杂度吧)
排序法
最差时间分析 平均时间复杂度 稳定度 空间复杂度 冒泡排序 O(n2) O(n2) 稳定 O(1) 快速排序 O(n2) O(n*log2n) 不稳定 O(log2n)~O(n) 选择排序 O(n2) O(n2) 稳定 O(1) 二叉树排序 O(n2) O(n*log2n) 不一顶 O(n) 插入排序
O(n2) O(n2) 稳定 O(1) 堆排序 O(n*log2n) O(n*log2n) 不稳定 O(1) 希尔排序 O O 不稳定 O(1) - 排序算法所要消耗额外内存的形式:
- 在原位(即原来占有的内存)进行排序的算法,除了使用一个小堆栈或表外,不需要任何额外的内存空间
- 使用链表表示或指针、数组索引来引用数据的排序算法,因此,需要额外的内存空间存储这个指针或索引即可
- 需要足够的额外空间来存储要排序的数组的副本数据
二、算法讲解与实现部分
1、简单选择排序
大致过程:首先,选出数组中最小的元素,将它与数组中第一个元素进行交换,然后找出次小的元素,并将它与数组中第二个元素进行交换。按照这种方法一直进行下去,知道整个数组排序完为止。图解如下:

代码如下:
void selectsort(int a[],int length){ int i, j; for (i = 0; i < length; i++) { int min = i; for (j = i + 1; j < length; j++) if (a[j] < a[min]) min = j; if (min != i) { int t = a[i]; a[i] = a[min]; a[min] = t; } }} 缺点:比较次数多,不能利用数据的已有序的特点,对已有序的部分依赖弱
优点:属于稳定排序,对于元素较大,但关键字又比较小的数据的排序,选择排序较适合
2、插入排序
大致思路:每次将一个待排序的元素与已排序的元素进行逐一比较,直到找到合适的位置按大小插入。

代码如下:
void insertion(int a[], int length){ int i, j; for (i = 1; i < length; i++) for (j = i; j > 0; j--) if (a[j - 1] > a[j]) { int t = a[j - 1]; a[j - 1] = a[j]; a[j] = t; }} 改进下:
void insertion(int a[], int length){ for (int i = 1; i < length; i++)//从第2个数据开始插入 { int j = i - 1; int t = a[i];//记录要插入的数据 while (j >= 0 && a[j] > t)//从后向前,找到比其小的数的位置 a[j + 1] = a[j--];//向后挪动 if (j != i - 1)//存在比其小的数 a[j + 1] = t; }} 优点:稳定,并且对数据的初始排列顺序很敏感,如果数据量很大时,且关键字已经部分排序,则插入排序速度比较快
缺点:对于顺序结构的数据,比较次数不一定,比较次数越少,插入点后的数据移动越多,特别是当数据总量庞大的时候。
3、冒泡排序
大致思路:遍历待排序的数据,如果邻近的两个元素大小顺序不对,就将二者进行交换操作,重复此操作直到所有数据排序好为止。图解如下:
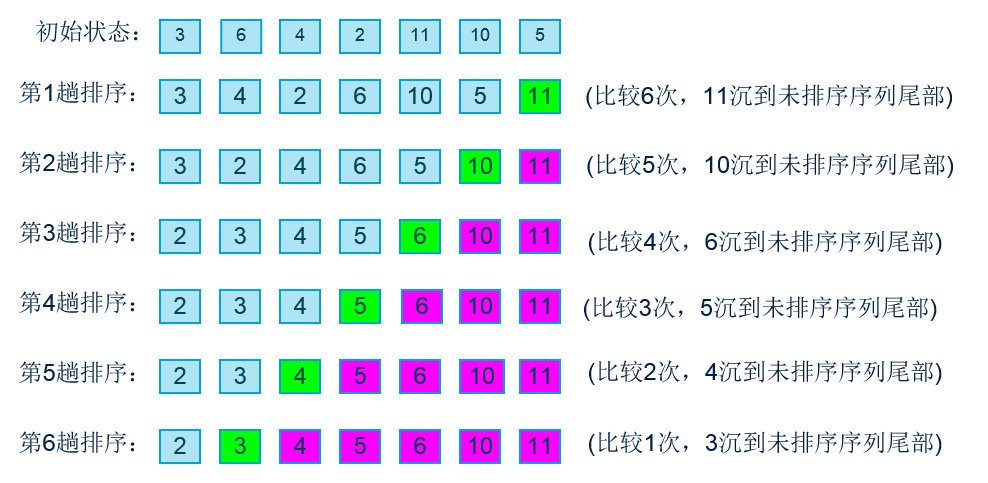
代码如下:
void bubble(int a[], int length){ for(int i=0;i i;j--) if(a[j-1]>a[j]) { int t = a[j]; a[j] = a[j - 1]; a[j - 1] = t; }} 改进:
void bubble(int a[], int length){ //如果a[0..i]已是有序区间,上次的扫描区间是a[i..length], //记上次扫描时最后一次执行交换的位置为pos, //则pos在i与length之间,则a[i..pos]区间也是有序的, //否则这个区间也会发生交换;所以下次扫描区间就可以由a[i..length] //缩减到[pos..n] int pos = 0, tpos = 0; for (int i = 0; i < length - 1; i++) { pos = tpos; for (int j = length - 1; j > pos; j--) { if (a[j - 1] > a[j]) { int t = a[j]; a[j] = a[j - 1]; a[j - 1] = t; tpos = j; } } //如果经过一次扫描后位置没变则表示已经全部有序 if (pos == tpos) break; }} 附上双向冒泡(抖动冒泡):
void ImpButtle(int a[], int length){ //先让冒泡排序由左向右进行,再来让冒泡排序由右往左进行"抖动"排序 int left = 0, right = length - 1, i, flag=0; while (left < right) { for(i=left;i a[i + 1]) { int t = a[i]; a[i] = a[i + 1]; a[i + 1] = t; flag = i; } right = flag; for(i=right;i>left;i--) if (a[i - 1] > a[i]) { int t = a[i - 1]; a[i - 1] = a[i]; a[i] = t; flag = i; } left = flag; }} (注:插入排序不能预知各个数据在数组中的最终位置,选择排序不会改变已排序好的数据的位置。插入排序每步中要平均移动已排序好的数据的一般长度,选择排序和冒泡排序每步都要访问所有尚未排序的数据,其中,冒泡排序将所有顺序不对的相邻的元素进行交换,而选择排序每步中只交换一次。
选择排序:N^2/2次比较操作 N次交换操作;插入排序:平均情况下,大约N^2/4次比较操作 N^2/4次交换操作,在最坏情况下都需要2倍的数量;冒泡排序:在平均和最坏情况下,执行大约N^2/2次比较操作和N^2/2次交换操作
对于数据项较大,关键字较小的数据,选择排序的运行时间是线性的)
4、希尔排序(缩小增量排序)
大致思路:是直接插入排序算法的一种更高效的改进版本。它允许非相邻的元素进行交换来提高执行效率。先取一个小于n的整数d1作为第一个增量,把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量![]() =1(
=1(![]() <
<![]() …<d2<d1),即所有记录放在同一组中进行直接插入排序为止。图解如下:
…<d2<d1),即所有记录放在同一组中进行直接插入排序为止。图解如下:

代码如下:
void Shellsort(int a[], int length){ for(int gap=length/2;gap>0;gap/=2)//此处步长每次减半 for(int i=gap;i = 0 && a[j] > a[j + gap]; j -= gap) { int t = a[j]; a[j] = a[j + gap]; a[j + gap] =t; }} 优点:快,数据移动少; 缺点:不稳定,d的取值是多少,应取多少个不同的值,都无法确切知道,只能凭经验来取(即不同的步长导致算法效率不同)。